【CF961E】Tufurama

E. Tufurama

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

One day Polycarp decided to rewatch his absolute favourite episode of well-known TV series "Tufurama". He was pretty surprised when he got results only for season 7 episode 3 with his search query of "Watch Tufurama season 3 episode 7 online full hd free". This got Polycarp confused — what if he decides to rewatch the entire series someday and won't be able to find the right episodes to watch? Polycarp now wants to count the number of times he will be forced to search for an episode using some different method.

TV series have n seasons (numbered 1 through n), the i-th season has a_i episodes (numbered 1 through a_i). Polycarp thinks that if for some pair of integers x and y (x < y) exist both season x episode y and season y episode x then one of these search queries will include the wrong results. Help Polycarp to calculate the number of such pairs!

Input

The first line contains one integer n (1  ≤ n  ≤  2·10⁵) — the number of seasons.

The second line contains n integers separated by space a₁, a₂, ..., a_n (1 ≤ a_i ≤ 10⁹) — number of episodes in each season.

Output

Print one integer — the number of pairs x and y (x < y) such that there exist both season x episode y and season y episode x.

Examples

input

5
1 2 3 4 5

output

0

input

3
8 12 7

output

3

input

3
3 2 1

output

2

Note

Possible pairs in the second example:

1.   x = 1, y = 2 (season 1 episode 2   season 2 episode 1);

2.   x = 2, y = 3 (season 2 episode 3   season 3 episode 2);

3.   x = 1, y = 3 (season 1 episode 3   season 3 episode 1).

In the third example:

1.   x = 1, y = 2 (season 1 episode 2   season 2 episode 1);

2.   x = 1, y = 3 (season 1 episode 3   season 3 episode 1).

题目大意：

• 1) i < j
• 2) a[i] >= j
• 3) a[j] >=i

显然地，大于 n 的 a[i] 可舍弃
对于给定的 j 位置，i < j 且 i <= a[j]
故 i ∈ [1, min(j - 1, a[j]]
为了满足 a[i] >= j，即求对于 i ∈ [1, min(j - 1, a[j]]，a[i] >= j 的个数

用个树状数组维护

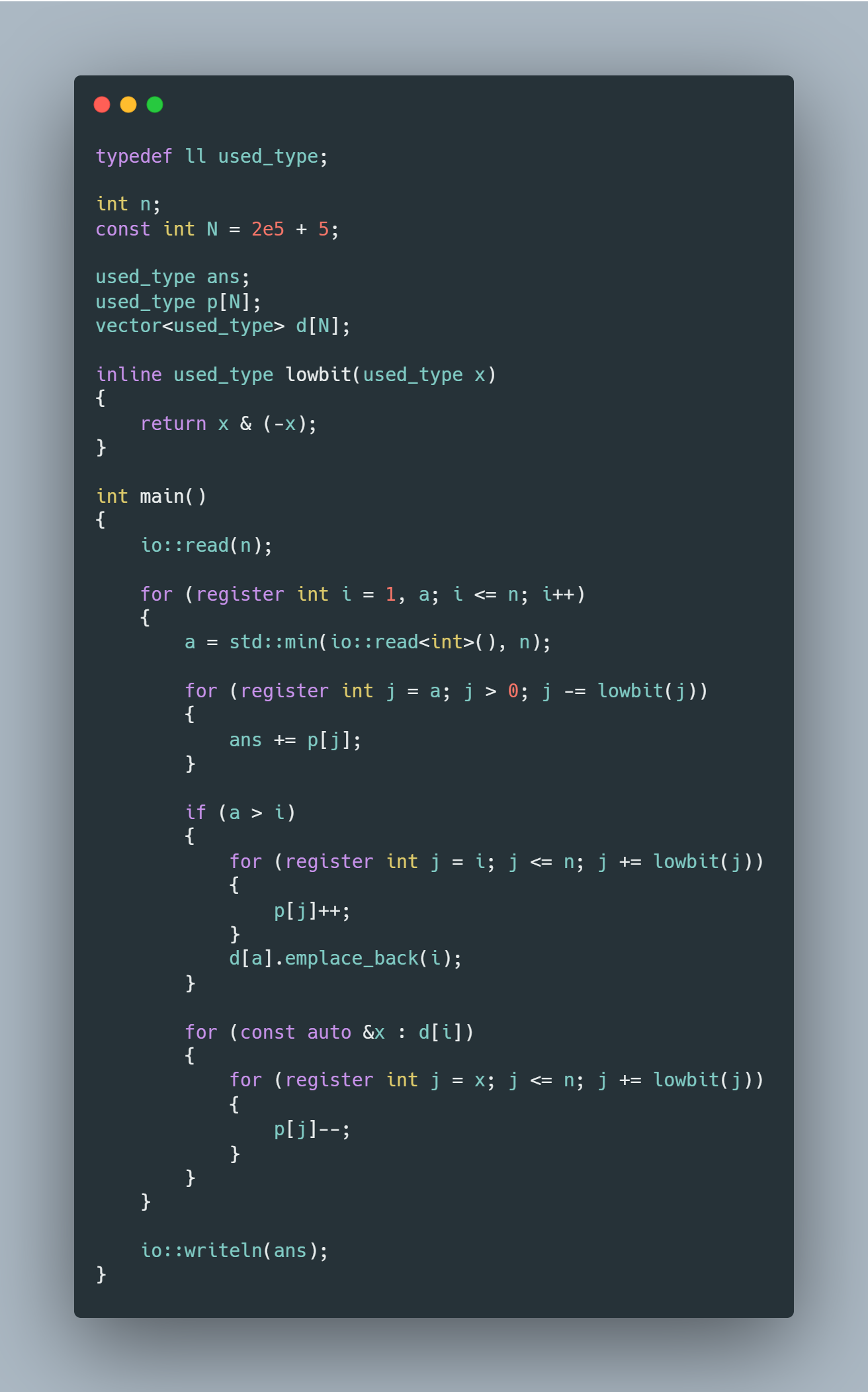
#pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math") #pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native") #include "bits/stdc++.h" #define mem(x) memset((x), 0, sizeof((x))) #define il __attribute__((always_inline)) using namespace std; typedef long long ll; typedef long double ld; typedef unsigned long long ull; #if __cplusplus > 201403L #define r #else #define r register #endif #define c const namespace _c { c double pi = acos(-1.0); namespace min { c int i8 = -128; c int i16 = -32768; c int i = -2147483647 - 1; c ll l = -9223372036854775807LL - 1; } // namespace min namespace max { c int i8 = 127; c int i16 = 32767; c int i = 2147483647; c ll l = 9223372036854775807LL; } // namespace max } // namespace _c namespace _f { template <typename T> inline c T gcd(T m, T n) { while (n != 0) { T t = m % n; m = n; n = t; } return m; } template <typename T> inline c T abs(c T &a) { return a > 0 ? a : -a; } template <typename T> inline T pow(T a, T b) { T res = 1; while (b > 0) { if (b & 1) { res = res * a; } a = a * a; b >>= 1; } return res; } template <typename T> inline T pow(T a, T b, c T &m) { a %= m; T res = 1; while (b > 0) { if (b & 1) { res = res * a % m; } a = a * a % m; b >>= 1; } return res % m; } } // namespace _f namespace io { template <typename T> inline T read() { r T res = 0, neg = 1; char g = getchar(); for (; !isdigit(g); g = getchar()) { if (g == '-') { neg = -1; } } for (; isdigit(g); g = getchar()) { res = res * 10 + g - '0'; } return res * neg; } template <typename T> inline void read(T &t) { t = read<T>(); } template <typename T> inline void readln(c T first, c T last) { for (r T it = first; it != last; it++) { read(*it); } } template <typename T> inline void _write(T x) { if (x < 0) { putchar('-'); x = -x; } if (x > 9) { _write(x / 10); } putchar(x % 10 + '0'); } template <typename T> inline void write(c T &x, c char &sep = ' ') { _write(x); putchar(sep); } template <typename T> inline void writeln(c T &x) { write(x, '\n'); } template <typename T> inline void writeln(c T first, c T last, c char &sep = ' ', c char &ends = '\n') { for (r T it = first; it != last; it++) { write(*it, sep); } putchar(ends); } #if __cplusplus >= 201103L template <typename T, typename... Args> void read(T &x, Args &... args) { read(x); read(args...); } #endif } // namespace io #undef c #undef r typedef ll used_type; int n; const int N = 2e5 + 5; used_type ans; used_type p[N]; vector<used_type> d[N]; inline used_type lowbit(used_type x) { return x & (-x); } int main() { io::read(n); for (register int i = 1, a; i <= n; i++) { a = std::min(io::read<int>(), n); for (register int j = a; j > 0; j -= lowbit(j)) { ans += p[j]; } if (a > i) { for (register int j = i; j <= n; j += lowbit(j)) { p[j]++; } d[a].emplace_back(i); } for (const auto &x : d[i]) { for (register int j = x; j <= n; j += lowbit(j)) { p[j]--; } } } io::writeln(ans); }