【CF961F】k-substrings

【CF961F】k-substrings

题意

给定一个长度为 n 的字符串 S
我们设 S 的 k-子串 是 S[k … n - k + 1]，设字符串 t 是字符串 T 的 奇正确前后缀 当且仅当满足以下条件：

• t 长度为奇数
• |t| < |T|
• t 是 T 的 border（既是前缀又是后缀）

对于 k = 1 … n / 2 上取整，求 S 的 k-子串 的最长 奇正确前后缀 长度。无解输出 -1
2 ≤ n ≤ 1,000,000

官方题解

1. 枚举某个前缀（指题目要求的相同前后缀中的前缀）的中心位置 i，那么对应后缀的中心位置已经确定了（n - i + 1），可以二分答案求出对于每个中心位置 i 最大的符合要求的相同前后缀（设长度为 2 * x + 1），然后更新 ans[i - x] 为 2 * x + 1；最后把每个 ans[i] 用 ans[i - 1] - 2 尝试更新一下
2. 其实以上做法也基于这个结论？
   ans[i - 1] <= ans[i] + 2，这个可以容易地用反证法证明（类似 kmp ）
   因此从 ans[(n + 1) / 2] 开始求就行了

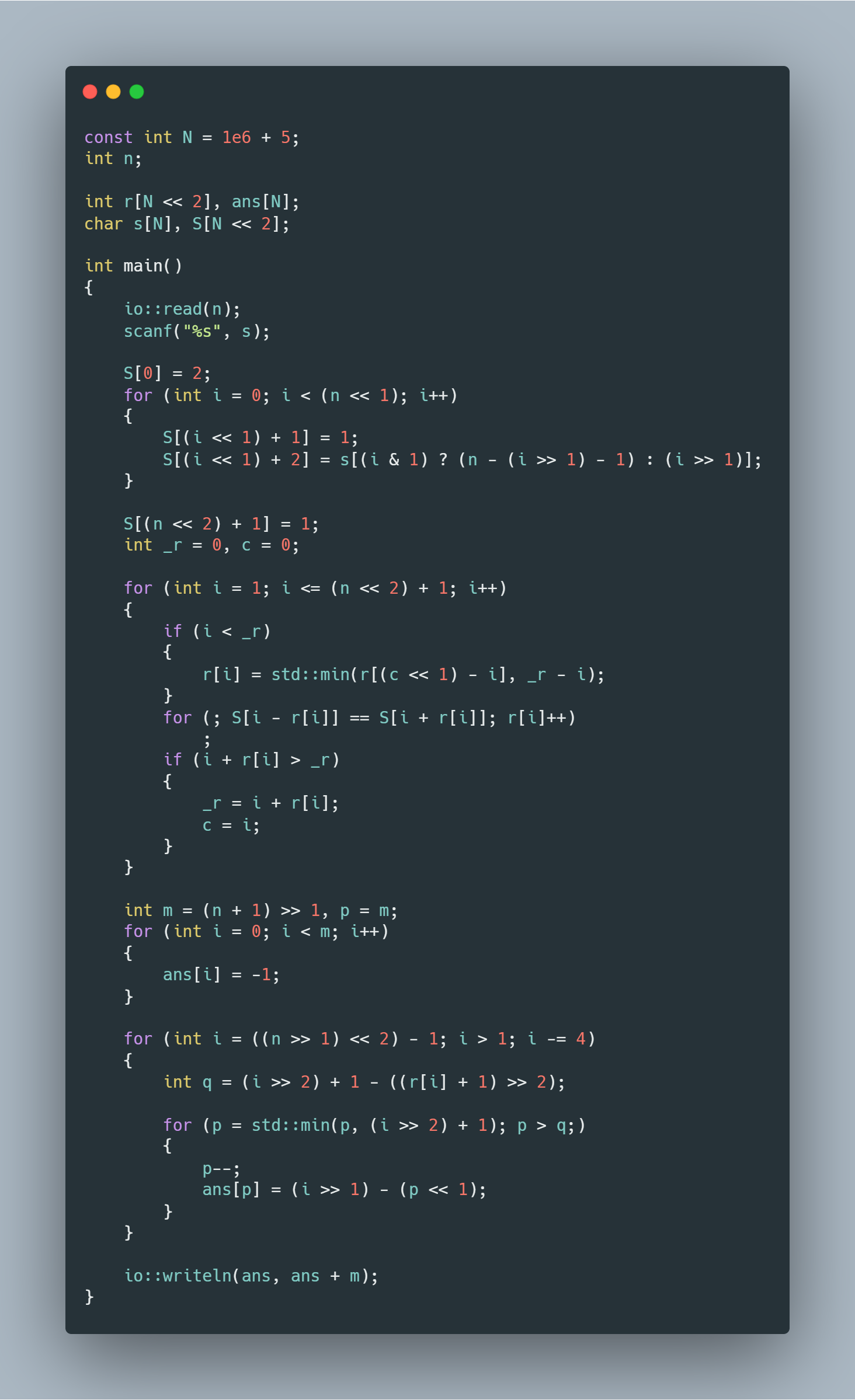
参考代码：

#pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")

#include "bits/stdc++.h"

#define mem(x) memset((x), 0, sizeof((x)))
#define il __attribute__((always_inline))

using namespace std;

typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;

#if __cplusplus > 201403L
#define r
#else
#define r register
#endif

#define c const

namespace _c
{
c double pi = acos(-1.0);
namespace min
{
c int i8 = -128;
c int i16 = -32768;
c int i = -2147483647 - 1;
c ll l = -9223372036854775807LL - 1;
} // namespace min

namespace max
{
c int i8 = 127;
c int i16 = 32767;
c int i = 2147483647;
c ll l = 9223372036854775807LL;
} // namespace max
} // namespace _c

namespace _f
{
template <typename T>
inline c T gcd(T m, T n)
{
    while (n != 0)
    {
        T t = m % n;
        m = n;
        n = t;
    }
    return m;
}

template <typename T>
inline c T abs(c T &a)
{
    return a > 0 ? a : -a;
}

template <typename T>
inline T pow(T a, T b)
{
    T res = 1;
    while (b > 0)
    {
        if (b & 1)
        {
            res = res * a;
        }
        a = a * a;
        b >>= 1;
    }
    return res;
}

template <typename T>
inline T pow(T a, T b, c T &m)
{
    a %= m;
    T res = 1;
    while (b > 0)
    {
        if (b & 1)
        {
            res = res * a % m;
        }
        a = a * a % m;
        b >>= 1;
    }
    return res % m;
}
} // namespace _f

namespace io
{
template <typename T>
inline T read()
{
    r T res = 0, neg = 1;
    char g = getchar();
    for (; !isdigit(g); g = getchar())
    {
        if (g == '-')
        {
            neg = -1;
        }
    }
    for (; isdigit(g); g = getchar())
    {
        res = res * 10 + g - '0';
    }
    return res * neg;
}
template <typename T>
inline void read(T &t)
{
    t = read<T>();
}
template <typename T>
inline void readln(c T first, c T last)
{
    for (r T it = first; it != last; it++)
    {
        read(*it);
    }
}

template <typename T>
inline void _write(T x)
{
    if (x < 0)
    {
        putchar('-');
        x = -x;
    }
    if (x > 9)
    {
        _write(x / 10);
    }
    putchar(x % 10 + '0');
}
template <typename T>
inline void write(c T &x, c char &sep = ' ')
{
    _write(x);
    putchar(sep);
}
template <typename T>
inline void writeln(c T &x)
{
    write(x, '\n');
}
template <typename T>
inline void writeln(c T first, c T last, c char &sep = ' ', c char &ends = '\n')
{
    for (r T it = first; it != last; it++)
    {
        write(*it, sep);
    }
    putchar(ends);
}

#if __cplusplus >= 201103L
template <typename T, typename... Args>
void read(T &x, Args &... args)
{
    read(x);
    read(args...);
}
#endif
} // namespace io
#undef c
#undef r

const int N = 1e6 + 5;
int n;

int r[N << 2], ans[N];
char s[N], S[N << 2];

int main()
{
    io::read(n);
    scanf("%s", s);

    S[0] = 2;
    for (int i = 0; i < (n << 1); i++)
    {
        S[(i << 1) + 1] = 1;
        S[(i << 1) + 2] = s[(i & 1) ? (n - (i >> 1) - 1) : (i >> 1)];
    }

    S[(n << 2) + 1] = 1;
    int _r = 0, c = 0;

    for (int i = 1; i <= (n << 2) + 1; i++)
    {
        if (i < _r)
        {
            r[i] = std::min(r[(c << 1) - i], _r - i);
        }
        for (; S[i - r[i]] == S[i + r[i]]; r[i]++)
            ;
        if (i + r[i] > _r)
        {
            _r = i + r[i];
            c = i;
        }
    }

    int m = (n + 1) >> 1, p = m;
    for (int i = 0; i < m; i++)
    {
        ans[i] = -1;
    }

    for (int i = ((n >> 1) << 2) - 1; i > 1; i -= 4)
    {
        int q = (i >> 2) + 1 - ((r[i] + 1) >> 2);

        for (p = std::min(p, (i >> 2) + 1); p > q;)
        {
            p--;
            ans[p] = (i >> 1) - (p << 1);
        }
    }

    io::writeln(ans, ans + m);
}