普通线段树

问题

给定长为$n$的序列A，有$m$次操作：

• ins x p：给A[x]增加p。
• ask l r：询问$A_{[l,r]}$的区间和。

$n,m\le 500000$.

分治

暴力显然是$O\left(nm\right)$的。我们来考虑分治。

假设我们查询$[1,1029]$的区间和。如果我们手上已经有$[1,1024]$的区间和，那么我们就把问题剖成了两段：$S(1,1029)=S(1,1024)+S(1025,1029)$. 这是可以很快得出结果的。

按照上面的思路，假设序列长度为$2048$，那么我们就把整个序列剖成$[1,1024],[1025,2048]$，然后进一步剖成$[1,512],[513,1024],[1025,1536],[1537,2048]$，这样剖下去，我们就把整个序列剖成了共$2n$个区间。

这就是线段树。

普通线段树

线段树是拥有分治结构的树。它长成这样（借个图）：

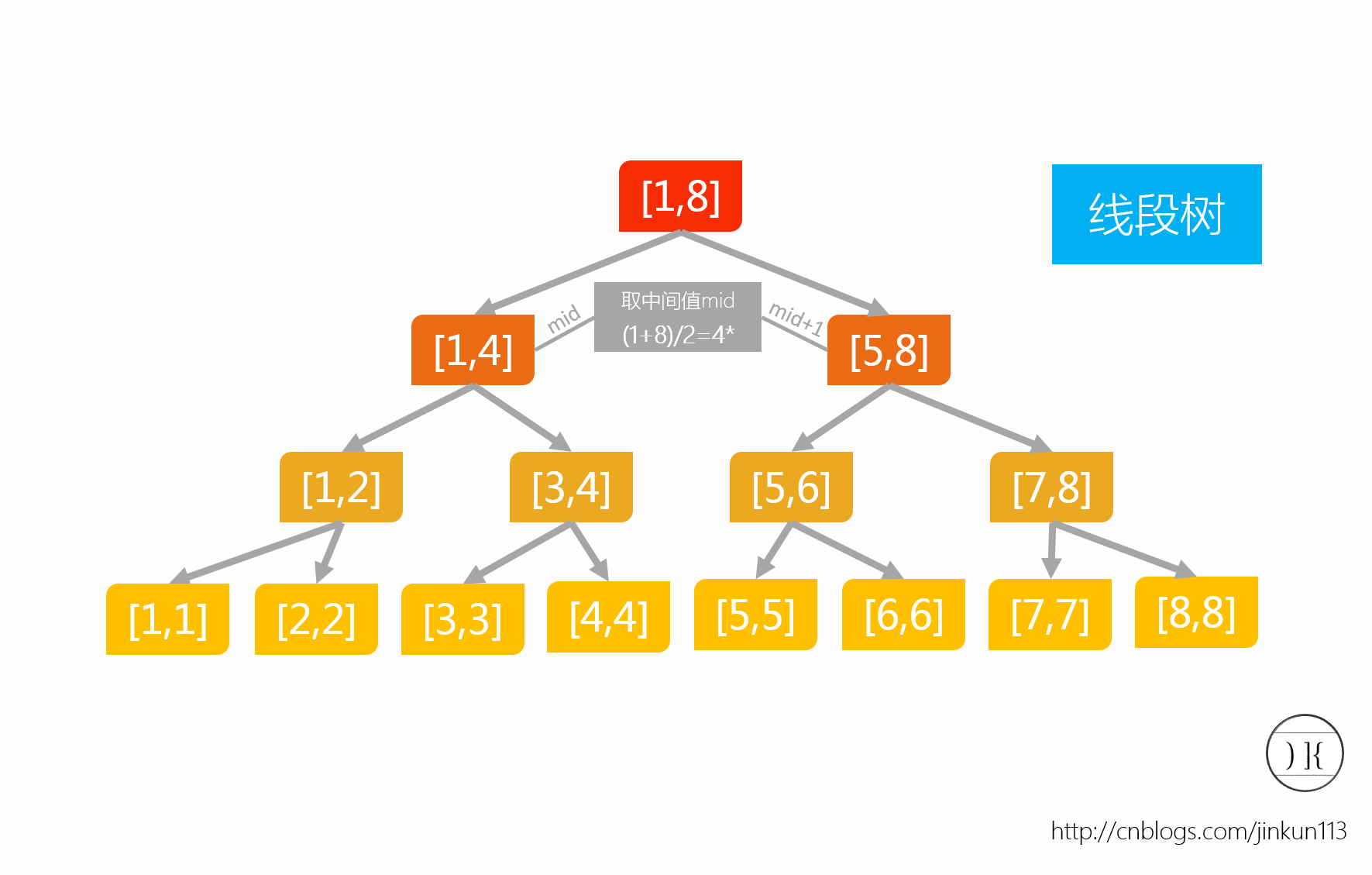
除了叶子节点，每个节点都有两个儿子。$[l,r]$的左儿子是$[l,mid]$，右儿子是$[mid+1,r]$.

那么题目中的操作就可以这样来处理：

添加操作：对于x，找到所有包含它的区间（共$\log n$个），给这些区间的和加上p。

查询操作则要困难一些。我们用一个递归过程实现它：

#define LE(x) ((x)*2)                   //用数组保存完全二叉树，x*2为x的左儿子，x*2+1为右儿子
#define RT(x) ((x)*2+1)

int L=1,R=1027;                         //L,R代表查询的区间
int ask(int x,int cl,int cr)            //cl,cr代表当前区间，x代表当前节点
{
    int mid=(cl+cr)/2;
    if(cl>R || cr<L) return 0;          //与这个区间毫不相干
    if(L<=cl && cr<=R) return sum[x];   //直接包含了这个区间

    return ask(LE(x),cl,mid)+ask(RT(x),mid+1,cr);
    //上述两种情况都不是，则返回两个儿子的查询结果
}

这样，一棵线段树就写出来啦！